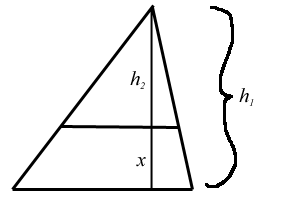
A couple of problems
The harder one first: Suppose you have a triangle. Your job is to draw a line within the triangle, parallel to the base, that creates a smaller triangle whose area is a given percentage of the area of the original. See the figure, in which all lines that look perpencular are perpendicular. (The line whose pieces are denoted by x and h2 is an altitude.)
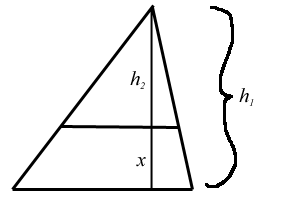
In other words, say I want the smaller triangle to have an area which is p% the area of the big triangle. What is x in terms of p? This can be done with simple Algebra and Geometry, and was brought to me by one of my tutoring students, R.J. Stuart. Here is the answer if you must cheat.
Now for the simple but cool one. Say you have a square, and you inscribe a circle inside it, then you inscribe
a square inside the circle:
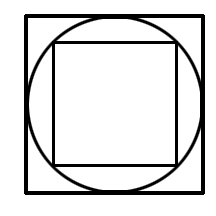
What is the area of the small square as compared to the area of the big square? Is this surprising? (Click here to cheat)
How about if you do it the other way around, with a circle inside a square inside a circle? Find the area of the small circle in relation to the area of the bigger one:
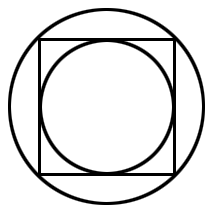
For all you Calculus students out there, what does this mean about the sum of the areas you'd get if you kept doing this, inscribing smaller and smaller circles inside of squares inside of circles inside of..., down to infinity? How does the sum of all the areas of all the inner circles compare to the area of the outermost circle? (Again, click here to cheat.) Also, note that you can do the same kind of problem using equilateral triangles or hexagons instead of squares, and come up with interesting (but not nearly as cool) results!
This is a fascinating result to me, and I'm sure there's some deep inner meaning here, given the fact that squares have rational area and circles have irrational area. Somebody please come up with some kind of philosophical justification of it all for me!
© 2000 Dan McGlaun